|
Usually associated with multimillion
dollar Cray supercomputers, vector processing is a powerful technique
for many applications. In this month's issue we will look at the
fundamental ideas behind this computing model, and discuss the future
outlook for this technology.
The issue of vector processing frequently raises the
question - does it have a future in this day and age of cheap commodity
general purpose processors ? Many observers see this technique as a
highly specialised computing technology which is worthless outside the
domains of simulating aerodynamics, quantum physics, chemistry,
supernovas, cryptography, geophysical data processing, finite element
analysis in structural engineering, synthetic aperture radar image
processing and other similar "heavy weight engineering / scientific"
applications.
As always, reality tends to be a little more complex
than the media and sales community would have us believe. Vector
processing is no exception in this respect.
What is Vector
Processing?
The idea of vector processing dates back to the 1960s, a
period which saw massive growth in the performance and capabilities of
mainframes, then the primary processing tools of the industry. Analysing
the performance limitations of the rather conventional CISC style
architectures of the period, it was discovered very quickly that
operations on vectors and matrices were one of the most demanding CPU
bound numerical computational problems faced.
A vector is a mathematical construct which is central to
linear algebra, which is the foundation of much of classical engineering
and scientific mathematics. The simplest physical interpretation of a
vector in 3 dimensional space is that it is an entity which is described
by a magnitude and a direction, which in a 3 dimensional space can be
described by 3 numbers, one for x, one for y and one for z. A vector [a
b c] is said to have 3 elements, and is stored in memory as an array.
Just as real numbers (float, double) and integers (int,
long) can be manipulated, so vectors can be manipulated, but the
operations are quite different.
-
Scaling - physically stretching or shrinking the
length of the vector, is done by multiplying each element in the vector
by the same scaling factor e.g. r*[a b c] == [ra rb rc].
-
Addition - creating a new vector by parallelogram
addition, is done by adding the respective first, second and third
elements e.g. [a b c] + [d e f] == [a+d b+e c+f].
These are the two most simple vector operations, and
readers with a science education will recall that vectors follow the
distributive, associative and commutative laws, so that many of the
basic tricks in algebra also hold for vector arithmetic.
However, vectors have distinct geometrical
interpretations as well, and this reflects in further types of
operations between vectors.
-
Dot Products - a number physically representing the
product of the length of two vectors multiplied by the cosine of the
angle between them, performed by multiplying the respective elements and
adding the products e.g. [a b c].[d e f] == ad + be + cf.
-
Cross Products - a vector perpendicular to two
vectors, found by taking the differences of products of the elements
e.g. [a b c]X[d e f] == [(bf-ce) (cd-af) (ae-bd)].
Needless to say, a large volume of mathematical theory
has grown out of vector algebra and calculus. As programmers what
interests us is the kind of structures and operations which are needed
to compute such problems.
What turns out to be of particular interest are matrices
and matrix operations, colloquially termed in the trade "matrix
bashing". Matrices provide some very convenient ways of representing and
solving systems of linear equations, or performing linear
transformations (functions) on vectors (scaling and changing the
direction of a vector).
A matrix in the simplest of terms is a two dimensional
array of coefficients, usually floating point numbers. Matrices can be
added, multiplied or scaled, and given some caveats, obey the laws of
association, commutation and distribution. What is important about
operations between matrices is that these operations mostly involve
multiplications, additions or dot and cross products between rows and
columns in the respective matrices.
This is very important from the perspective of machine
arithmetic, since operations between rows and columns amount to
primitive vector operations. Therefore inside the machine they can be
represented with a single operation code (opcode) ad one dimensional
arrays of operands.
Consider the choices we have in building hardware to
compute say an addition between two vectors. On a conventional machine
we must perform N individual operand loads into registers, N additions
and N stores for two N sized vectors. Each load. addition and store
incurs an opcode fetch cycle and all of the heartache of shuffling the
operands around in the CPU.
The alternative is to add an instruction into the
machine which says "ADD, N, A, B, C", or add N element vectors A and B
and store the result into vector C, where operands A, B and C are
pointers to the memory addresses of arrays A, B and C. Doing it this way
achieves several desirable things - we use only one opcode no matter how
big N is, thereby saving a lot of bus bandwidth and decoder time, and
we end up with a repetitive run of identical operations, here loads,
adds and stores, which means that in a pipelined CPU we minimise the
number of pipeline stalls and thus lost performance. The bigger the
length of the vector, the better, although in practice additional little
gain is seen for vector sizes bigger than 10-20.
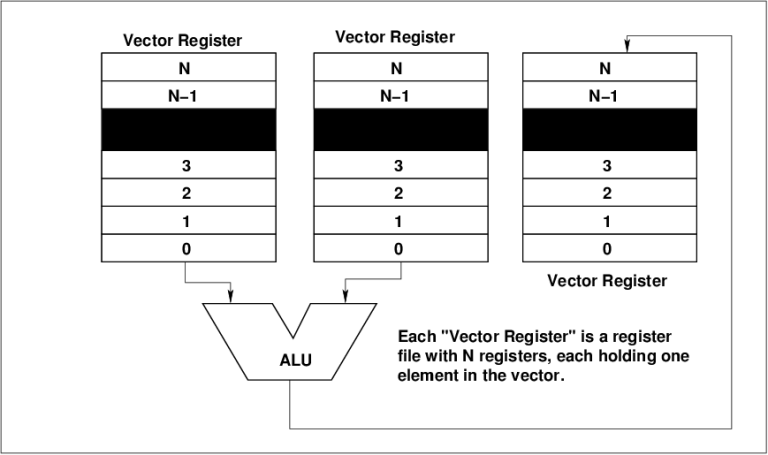
Processing vector operands (C. Kopp)
This is the central idea behind vector processors and
why they can achieve significantly better performance than their general
purpose cousins - by collapsing large numbers of basic operations into
single vector operations which involve repeated bursts of identical
primitive operations.
Of course, a vector processor built around the internal
architecture of a general purpose pipelined CPU, which merely includes
extra microcode or control logic to execute vector instructions, will
more than likely deliver at most several times the performance of its
mundane cousin. Even a Cray 1 delivers only about an 8 fold performance
improvement between its vector and scalar hardware (actually superscalar
hardware - as a minor diversion, the term superscalar would appear to
have its origins in the supercomputing world, where the use of multiple
execution units for scalar problems needed a decent buzzword !), on
typical computations compiled using either vector or conventional/scalar
operations.
To get genuinely blinding improvements in speed, it is
necessary to optimise the architecture to facilitate vector operations.
This amounts to organising the storage in a manner which makes it easy
to quickly load and store array operands, or in other terms, the
bandwidth between the CPU and main memory must be maximised, and the
bandwidths between operands and execution units in the CPU must be
maximised.
Various techniques have been used over the last 4
decades to achieve this. The brute force approach, is to put a very wide
and fast bus between the main memory and the CPU, and use the fastest
RAM you can buy. This approach is particularly attractive if you are
working with very large vectors which have dozens or hundreds of
elements, since the CPU can crunch away to its heart's content sucking
vector elements directly into the execution unit load registers.
The cheaper approach, used in the Cray 1 and early
Control Data machines, is to put a very large block of "scratch-pad"
memory into the CPU as a vector operand register bank (file), or "vector
registers". Since the preferred format of vector instructions uses three
operands, two sources and one destination for the result, this register
bank usually ends up being split into three or more parts.
To execute a vector instruction with an vector length
which fits into the vector register bank, the two source operand arrays
are sucked into the registers. Then the execution unit grinds its way
through the instruction, leaving the result vector in the reserved area
of vector register bank. It can then be copied back into memory.
This strategy works wonderfully until the vector length
is larger than the vector register array length. At that point, the CPU
has to chop the operation into multiple passes, since it can only work
through a single register bank's worth of operands at a time. So it will
go through a load cycle, vector compute cycle, store cycle, then
another load cycle, etc, repeating this process until the whole vector
operation is completed. Every time the CPU has to do an intermediate
store and load of the vector register bank, the execution unit is idling
and no work gets done. This is the classical "fragmentation" problem,
since every time the vector operand overruns a multiple of the vector
register array's size, the time overhead of a load and store cycle for
the whole vector register array is incurred.
My favourite illustration of this is the famous curve of
Cray 1 MegaFLOPS performance vs the dimensions of two matrices being
multiplied. The Cray 1 has vector registers sized at 64. For a matrix
size of up to about twenty, the MFLOPS shoot up almost linearly to about
80 MFLOPS, upon which the speedup slows down to 132 MFLOPS for 64x64
matrices. Then the MFLOPS dip down to about 100, since the registers
have to be reloaded again, after which they creep up to 133 MFLOPS at
128x128, and this repeats on and on at multiples of 64.
The only way to work around this problem is to make the
vector register banks bigger, which costs extra bucks.
Clearly the biggest performance killer in such a vector
processor is the need to reload the vector register banks with operands.
There do however exist situations where a particular trick, termed
"chaining", can be used to work around this.
Consider a situation where you are manipulating a
vector, and then manipulating the resulting vector, and so on, and the
vector fits inside a vector register array. What this means is that the
result vector from one vector instruction, becomes one of the input
operands for a subsequent vector instructions. Why bother storing it out
into memory and then loading it back into the CPU again ?
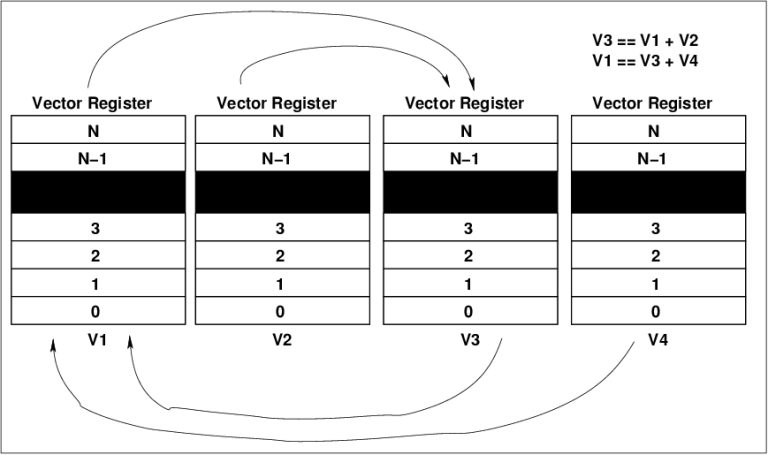
Chaining in a vector processor (C. Kopp)
Chaining involves managing the use of the vector
register arrays in the register bank in a manner which minimises the
number of redundant load-store cycles on vector operands. A three vector
operand instruction set (opcode, source1, source2, result) requires a
minimum of three vector register arrays, so any number of additional
vector register arrays above this facilitates chaining. The venerable
Cray 1 used four. If your CPU is well organised internally, and uses
chaining, then it is feasible to then load a vector register array with
a vector operand for a subsequent instruction, while the execution unit
is busily crunching away on the remaining three vector registers, doing
the current instruction. Once it has finished that vector instruction,
it starts the next with the two operands already sitting in the vector
registers. If the following vector instruction can also be chained, then
its vector operand can be loaded into the unused four vector register.
Chaining works best if the time to load a vector
register array is equal or shorter than the time to execute a vector
instruction. This is one of the reasons why main memory bandwidth, both
in terms of RAM speed and bus speed, suffers little compromise in a
supercomputer.
Getting Bang for Your
Buck
Extracting value for money out of vector processing
hardware depends very much upon the problem you are trying to solve, the
compiler you have, and the idiosyncrasies of the vector hardware on your
machine.
If your purpose in life is to deal with the "classical
supercomputing" problems which involve mostly large matrix operations,
then vector processors like Crays are the best approach. The basic
problem is rich in primitive vector operations and the machine can be be
driven to its best.
In practice, most problems involve a mix of scalar and
vector computations. However,it turns out that even in solving a scalar
problem the vector hardware might be used to an advantage. Instruction
Level Parallelism (ILP) is the cornerstone of squeezing extra
performance out of conventional superscalar processors, by concurrently
executing consecutive instructions which have no mutual dependencies.
This idea can be frequently exploited in a vector
processor. Consider a loop with a large number of passes, in which
several computations have no mutual dependency - what is computed in one
pass through the loop in no way affects any other pass. If you have a
vector processor, then your compiler can cleverly arrange to compute all
of the these instructions on the vector unit rather than as consecutive
passes through the scalar unit. This technique for parallelising loops
when possible is usually credited to the original Cray Fortran
compiler.
So vector hardware is not necessarily a dead loss in
areas outside its primary role. Exploiting it properly does require
proper compiler support, and also a suitable language. Fortran was
designed for matrix bashing and has superb support for arrays and
complex numbers. C and C++, despite being well designed for system
programming and many other application areas, has quite primitive
support for arrays. A recent proprietary improvement has been a C
compiler for Digital Signal Processing (DSP) chips, with language
extensions to support complex numbers.
The native vector size of the vector processing hardware
is also an issue, as noted previously. If you are to perform operations
on large vectors, then a machine native vector size must also be large.
However, many situations do arise where a short vector
size is perfectly adequate. The most obvious of these is in the
processing of 3D graphics, where images must be rotated, scaled and
translated. All of these operations map very efficiently into floating
point vector operations with 3 element long vectors. Signal and image
processing are other areas of interest, since they also present
opportunities for vectorisation.
The central issue is however the ability of the
compiler, or hand crafted assembler libraries, to transform the
primitive vector operations in the application code into a format
compatible with the hardware. Sometimes the vector operations are
obvious, other times such as in the parallelising of loops, not so
obvious.
The caveat for end users is therefore to properly
understand their application and tools, before spending on a processor
with vector hardware in it. A tale I have cited in the past is the user
who went out and bought a "vector co-processor box" only to find that
his application did not vectorise well.
Vector Processing
Products
The most famous and traditionally least affordable
vector processors in the market are Seymour Cray's machines. Cray was a
senior machine architect at Control Data Corporation, who was heavily
involved in the development of their supercomputing mainframes, which
pretty much dominated the scientific supercomputing market of the mid to
late sixties. Cray subsequently departed CDC and set up his own shop.
His first machine was the Cray 1, which proved to be stunning success in
the market. A characteristic feature of early Crays was the use of a
very fast bus, and a circular machine layout around what amounted to a
backplane wrapped around a cylinder. This was done to minimise the
length and clock cycle time of the main bus to memory.
The Cray 1 used a combination of superscalar and vector
techniques and outperformed its competitors with a then stunning 133
MFLOPS of floating point performance. It was released in 1976 and the
first unit went to Los Alamos, presumably to crunch away on hydrodynamic
simulations of nuclear bomb implosions.
The successor to the Cray 1 was the Cray 2, with 1.9
GigaFLOPS of performance and up to 2 GB or very fast main memory, it was
released in 1985.
The Cray X-MP was the first multiprocessing Cray,
released in 1982, with a modest 500 MFLOPS of performance and the Unix
derived Unicos operating system. It was followed in the late eighties by
the Y-MP series, which cracked the 1 GFLOPS barrier for this machine
family, later models used up to 8 vector processors.
The end of the Cold War brought hard times for Cray, as
the primary market, Defence Department and defence contractors,
collapsed very rapidly. During the nineties, Cray was purchased by
Silicon Graphics, Inc., who found that owning the famous name did not
return the profits they anticipated. Earlier this year, Tera Computer
Company, based in Seattle, closed a deal with SGI and acquired Cray for
around US $50.00M and one million shares. Tera, with a product base in
supercomputing, subsequently renamed themselves Cray Inc.
The merged product line now carries the Cray brand name,
and includes the SV1, SV2, T3 and T90 series machines, merging the
previous SGI product lines with the Tera product lines.
The most notable of these machines is the Scalable
Vector 1 (SV1) family, which is claimed to provide 1.9 GFLOPS in a
Single Streaming Processor, and 4.8 GFLOPS in a Multi-Streaming
Processor. Up to 32 such systems can be clustered.
Whether the new look Cray Inc. can recapture market
position and mystique of Seymour Cray's original series remains to be
seen - the decade is yet young.
Another product which was popular during the early
nineties, especially for embedded and military applications, was the
Intel i860 microprocessor family. The i860 is not a "true" vector
processing machine, with only 1 million transistors and a clock speed of
40 MHz it was a modest product by high performance computing standards.
What distinguished it from its contemporaries was its heavily pipelined
floating point hardware, which in its "pipelined" mode of operation
could deliver up to 80 MFLOPS single precision and 60 MFLOPS double
precision. Widely touted as a "Cray on a chip", the i860 ended up
becoming a niche number crunching processor in various add-on boxes, and
a DSP substitute in Multibus and VMEbus boards. Against the commodity
microprocessors of its day, it was an exceptional performer. However
the need to switch it into the "vector" pipelined mode meant that many
people considered it hard to code for. Usually libraries were supplied
and applications had to be ported across, unlike the elegant Cray
Fortran compilers. The chip was recently obsoleted and is a legacy item.

(Images - Motorola)
The currently "kewl" item in the commodity processor
market is the PowerPC G4 chip, from the IBM/Apple/Motorola consortium.
This machine is being marketed as a "superscalar processor with a vector
co-processor", running at twice the speed of equivalent Pentiums, to
cite Apple. Given that the chip has only about 1/3 to 1/2 the number of
transistors than its competitors in the Intel world have, this is indeed
an ambitious claim.
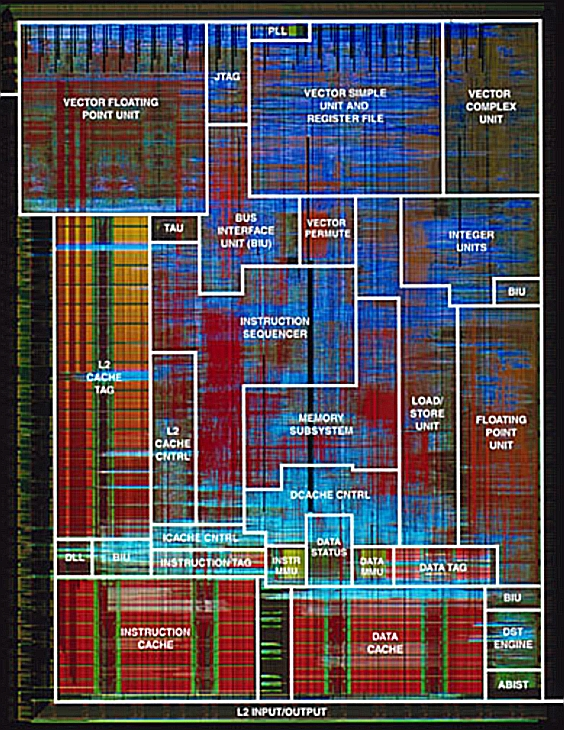
The MPC7400 chip is indeed a genuine vector processing
machine, with a PowerPC superscalar core extended with a "short vector"
co-processor and additional AltiVec vector instructions (See Figure 1.).
The AltiVec vector hardware is optimised for graphics and signal
processing applications, and occupies almost one third of the die (see
Figure 2.). The vector unit is 128 bits wide, and can operate on vector
sizes of 4 with single precision floating point operands, or 8 with
16-bit integers, or 16 with 8-bit operands. The vector register file has
32 128-bit entries, which can be accessed as 8, 16 or 32 bit operands,
equivalent to 1/4 of the original Cray 1. No less than 162 AltiVec
instructions are available in the machine instruction set.
The AltiVec hardware is not intended to fill the
Cray-like niche of heavy weight engineering / scientific computation,
but is clearly well sized to deliver in its primary niche of graphics,
multimedia and signal processing, areas which can frequently stretch
current superscalar CPUs.
Apple's performance claims of "a 500 MHz G4 is 2.2 times
faster than an 800 MHz P-III" upon closer examination refer specifically
to operations such as FFTs, convolutions, FIR filters, dot products and
array multiplications, with a peak performance gain of 5.83 times for,
surprise, surprise, a 32 tap convolution operation on a 1024 element
array. Other than some slightly dubious clock speed scalings, the Apple
numbers are what you would expect, indeed FFT performance is almost the
same for both CPUs. So unless your application uses the AltiVec
instruction set generously, do not expect dramatic performance
advantages !
From a technology viewpoint the AltiVec G4 shows that it
is now pretty much feasible to pack the architectural equivalent of a
Cray 1 on to a single die. Anybody care for a desktop 1.2 GHz Crayette?
|
![Home - Air Power Australia Website [Click for more ...]](APA/APA-Title-Main.png)
![Sukhoi PAK-FA and Flanker Index Page [Click for more ...]](APA/flanker.png)
![F-35 Joint Strike Fighter Index Page [Click for more ...]](APA/jsf.png)
![Weapons Technology Index Page [Click for more ...]](APA/weps.png)
![News and Media Related Material Index Page [Click for more ...]](APA/media.png)
![Surface to Air Missile Systems / Integrated Air Defence Systems Index Page [Click for more ...]](APA/sams-iads.png)
![Ballistic Missiles and Missile Defence Page [Click for more ...]](APA/msls-bmd.png)
![Air Power and National Military Strategy Index Page [Click for more ...]](APA/strategy.png)
![Military Aviation Historical Topics Index Page [Click for more ...]](APA/history.png)
![Intelligence, Surveillance and Reconnaissance and Network Centric Warfare Index Page [Click for more ...]](APA/isr-ncw.png)
![Information Warfare / Operations and Electronic Warfare Index Page [Click for more ...]](APA/iw.png)
![Systems and Basic Technology Index Page [Click for more ...]](APA/technology.png)
![Related Links Index Page [Click for more ...]](APA/links.png)
![Homepage of Australia's First Online Journal Covering Air Power Issues (ISSN 1832-2433) [Click for more ...]](APA/apa-analyses.png)
![Home - Air Power Australia Website [Click for more ...]](APA/APA-Title-Main.png)
![Sukhoi PAK-FA and Flanker Index Page [Click for more ...]](APA/flanker.png)
![F-35 Joint Strike Fighter Index Page [Click for more ...]](APA/jsf.png)
![Weapons Technology Index Page [Click for more ...]](APA/weps.png)
![News and Media Related Material Index Page [Click for more ...]](APA/media.png)
![Surface to Air Missile Systems / Integrated Air Defence Systems Index Page [Click for more ...]](APA/sams-iads.png)
![Ballistic Missiles and Missile Defence Page [Click for more ...]](APA/msls-bmd.png)
![Air Power and National Military Strategy Index Page [Click for more ...]](APA/strategy.png)
![Military Aviation Historical Topics Index Page [Click for more ...]](APA/history.png)
![Intelligence, Surveillance and Reconnaissance and Network Centric Warfare Index Page [Click for more ...]](APA/isr-ncw.png)
![Information Warfare / Operations and Electronic Warfare Index Page [Click for more ...]](APA/iw.png)
![Systems and Basic Technology Index Page [Click for more ...]](APA/technology.png)
![Related Links Index Page [Click for more ...]](APA/links.png)
![Homepage of Australia's First Online Journal Covering Air Power Issues (ISSN 1832-2433) [Click for more ...]](APA/apa-analyses.png)
![Sukhoi PAK-FA and Flanker Index Page [Click for more ...]](APA/flanker.png)
![F-35 Joint Strike Fighter Index Page [Click for more ...]](APA/jsf.png)
![Weapons Technology Index Page [Click for more ...]](APA/weps.png)
![News and Media Related Material Index Page [Click for more ...]](APA/media.png)
![Surface to Air Missile Systems / Integrated Air Defence Systems Index Page [Click for more ...]](APA/sams-iads.png)
![Ballistic Missiles and Missile Defence Page [Click for more ...]](APA/msls-bmd.png)
![Air Power and National Military Strategy Index Page [Click for more ...]](APA/strategy.png)
![Military Aviation Historical Topics Index Page [Click for more ...]](APA/history.png)
![Information Warfare / Operations and Electronic Warfare Index Page [Click for more ...]](APA/iw.png)
![Systems and Basic Technology Index Page [Click for more ...]](APA/technology.png)
![Related Links Index Page [Click for more ...]](APA/links.png)
![Homepage of Australia's First Online Journal Covering Air Power Issues (ISSN 1832-2433) [Click for more ...]](APA/apa-analyses.png)